In my research I mostly work with the Julia programming language and most of the software I produce tends to be different kinds of Julia packages. You can find most of my packages on GitHub, some of the more important ones are also listed below.
General purpose packages
These packages are intended to be used in multiple settings and could potentially be useful for other people as well.
Arblib.jl
Arblib is a Julia package in the public repository which aims to be a thin and efficient wrapper around Arb - a C library for arbitrary-precision ball arithmetic. I’m one of the main developers, together with Marek Kaluba and Sascha Timme.
ArbExtras.jl
ArbExtras is a Julia package in the public repository that extends Arblib with basic tools for rigorous numerics that I found useful in many of my projects. Among other things it contains methods enclosing roots, enclosing extrema and computing integrals.
Project specific packages
These packages were developed specifically for one, or possibly a few, projects. They generally have an accompanying paper which gives the context.
CGL.jl
The computer assisted proof accompanying the paper
Dahne, J., Figueras, J-L. Self-similar Singular Solutions to the Nonlinear Schrödinger and the Complex Ginzburg-Landau Equations (2024). [arXiv]
HighestCuspedWave.jl
The computer assisted proof accompanying the paper
Dahne, J.. Highest Cusped Waves for the Fractional KdV Equations. Journal of Differential Equations, 401, 550-670 (2024). [DOI]
BurgersHilbertWave.jl
The computer assisted proof accompanying the paper
Dahne, J. & Gómez-Serrano, J.. Highest Cusped Waves for the Burgers-Hilbert Equation. Archive for Rational Mechanics and Analysis, 247(5) (2023). [DOI]
PaynePolygon.jl
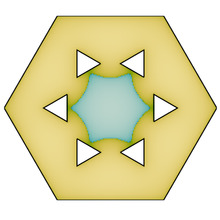
The computer assisted proof accompanying the paper
Dahne, J., Gómez-Serrano, J., & Hou, K.. A counterexample to Payne’s nodal line conjecture with few holes. Commun. Nonlinear Sci., 103(), 105957 (2021). [DOI]
MethodOfParticularSolutions.jl
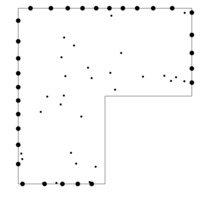
A package for computing eigenvalues and eigenfunctions of the Laplacian on planar or spherical domains using the method of particular solutions. Primarily for use in the papers
- Dahne, J., Gómez-Serrano, J., & Hou, K.. A counterexample to Payne’s nodal line conjecture with few holes. Commun. Nonlinear Sci., 103(), 105957 (2021). [DOI]
- Dahne, J., & Salvy, B., Computation of tight enclosures for laplacian eigenvalues, SIAM Journal on Scientific Computing, 42(5), 3210–3232 (2020). [DOI]